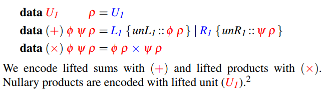Instances for everyone, free, and let no one go unsatisfied

Generic programming in Haskell

Alexey Kotlyarov

@koterpillar

data User = User
  { name :: Text
  , email :: Text
  } deriving (Ord, Eq, Show)
show $ User "Spike" "spike@mail.mars"
-- "User {name = \"Spike\", email = \"spike@mail.mars\"}"

Where does this instance come from, and how to make more?

data Bit = O | I

class ToBits a where
  toBits :: a -> [Bit]
data Unit = Unit

instance ToBits Unit where
  toBits Unit = []
data Sum a b = First a | Second b

instance (ToBits a, ToBits b) => ToBits (Sum a b) where
  toBits (First a) = O:toBits a
  toBits (Second b) = I:toBits b
data Product a b = Product a b

instance (ToBits a, ToBits b) => ToBits (Product a b) where
  toBits (Product a b) = toBits a ++ toBits b
Type         Isomorphic to
() Unit
Maybe a Sum Unit a
[a] Sum Unit (Product a [a])
User Product Text Text

To write an instance for any data type:

  • Write all instances in terms of Unit, Sum and Product.
  • Build an isomorphism between our types and those three.
class Generic a where
  type Rep a
  from :: a -> Rep a
  to :: Rep a -> a

...but we still can't write a Show!

data Maybe a = Just { fromJust :: a } | Nothing
data Option a = Some { fromSome :: a } | None

The set of values is the same, yet the types are different.

-- Phantom type level strings
data Data (n :: Symbol) a = Data a
data Constructor (n :: Symbol) a = Constructor a
data Selector (n :: Symbol) a = Selector a

dataName :: KnownSymbol n => Data n a -> String
constructorName :: KnownSymbol n => Constructor n a -> String
selectorName :: KnownSymbol n => Selector n a -> String
Type   Representation
() Data "()" (Constructor "()" Unit)
Maybe a Data "Maybe" (Sum (Constructor "Nothing" Unit) (Constructor "Just" a))
[a] Data "[]" (Sum (Constructor "[]" Unit) (Constructor ":" (Product a [a])))
User Data "User" (Constructor "User" (Product (Selector "name" Text) (Selector "email" Text)))

GHC.Generics

data U1 p = U1  -- Unit
data (:+:) f g p = L1 (f p) | R1 (g p)  -- Sum
data (:*:) f g p = (f p) :*: (g p)  -- Product

data R
newtype K1 i c p = K1 { unK1 :: c }  -- Value of type c
type Rec0 = K1 R
Type       Representation so far
() U1
Maybe Int U1 :+: Rec0 Int
User Rec0 Text :*: Rec0 Text

p is a phantom type parameter used later.

GHC.Generics

data D
data C
data S
newtype M1 i (c :: Meta) f p = M1 { unM1 :: f p }
type D1 = M1 D  -- Data type
type C1 = M1 C  -- Constructor
type S1 = M1 S  -- Selector
Type       Representation so far
() D1 _ (C1 _ U1)
Maybe Int D1 _ (C1 _ U1 :+: C1 _ (S1 _ (Rec0 Int)))
User D1 _ (C1 _ (S1 _ (Rec0 Text) :*: S1 _ (Rec0 Text)))

Meta is information about the type name, laziness, etc.

GHC.Generics

datatypeName :: Datatype m => d m f p -> String
conName :: Constructor m => c m f p -> String
selName :: Selector m => s m f p -> String

In practice:

datatypeName :: D1 m f p -> String
conName :: C1 m f p -> String
selName :: S1 m f p -> String

Writing an instance

data User = User
  { name :: Text
  , email :: Text
  } deriving (Generic)
λ> :kind! (Rep User)
(Rep User) :: * -> *
= D1
    ('MetaData "User" "Main" "main" 'False)
    (C1
       ('MetaCons "User" 'PrefixI 'True)
       (S1
          ('MetaSel
             ('Just "name")
             'NoSourceUnpackedness
             'NoSourceStrictness
             'DecidedLazy)
          (Rec0 Text)
        :*: S1
              ('MetaSel
                 ('Just "email")
                 'NoSourceUnpackedness
                 'NoSourceStrictness
                 'DecidedLazy)
              (Rec0 Text)))

kind! on GHCi prompt is most useful when working with generics.

Writing an instance

data User = User
  { name :: Text
  , email :: Text
  } deriving (Generic)
λ> from $ User "Spike" "spike@mail.mars"
M1 {unM1 = M1 {unM1 = M1 {unM1 = K1 {unK1 = "Spike"}} :*:
           M1 {unM1 = K1 {unK1 = "spike@mail.mars"}}}}

λ> from $ Just 1
M1 {unM1 = R1 (M1 {unM1 = M1 {unM1 = K1 {unK1 = 1}}})}
  • Both values have three M1 wrappers corresponding to the data type, the constructor and the selector.
  • Note :*: in the product type and R1 in the sum type.

Writing an instance

type FormData = Map Text [Maybe Text]  -- a=1&b=2&b=3&c&c=4

class ToFormData a where
  toFormData :: a -> FormData

Modifying to use generic instances:

class ToFormData a where
  toFormData :: a -> FormData
  {- Default implementation for the types meeting these requirements -}
  default toFormData :: (Generic a, ToFormData' (Rep a)) => a -> FormData
  toFormData = toFormData' . from

class ToFormData' r where
  toFormData' :: r p -> FormData

Writing an instance

Base case, single value:

-- instance ToFormData' (Rec0 Text) where
--   toFormData' (K1 a) = error "We can't write this without the selector name!"

instance Selector s => ToFormData' (S1 s (Rec0 Text)) where
  toFormData' m@(M1 (K1 a)) = M.singleton (T.pack $ selName m) [Just a]

Product and sum:

instance (ToFormData' f, ToFormData' s) => ToFormData' (f :*: s) where
  toFormData' (a :*: b) = M.union (toFormData' a) (toFormData' b)

instance (ToFormData' l, ToFormData' r) => ToFormData' (l :+: r) where
  toFormData' (L1 l) = toFormData' l
  toFormData' (R1 r) = toFormData' r

Ignore the rest of the meta:

instance ToFormData' f => ToFormData' (D1 m f) where
  toFormData' (M1 a) = toFormData' a

instance ToFormData' f => ToFormData' (C1 m f) where
  toFormData' (M1 a) = toFormData' a

Writing an instance

data User = User
  { name :: Text
  , email :: Text
  } deriving (Generic, ToFormData)
  • GHC can derive an implementation of Generic...
  • Which satisfies ToFormData'...
  • ...so ToFormData does not need any methods.

Alternatively:

instance ToFormData User
-- No methods

Writing an instance

class FromFormData a where
  fromFormData :: FormData -> Maybe a
  default fromFormData :: (Generic a, FromFormData' (Rep a)) => FormData -> Maybe a
  fromFormData = fmap to . fromFormData'

class FromFormData' a where
  fromFormData' :: Map Text [Maybe Text] -> Maybe (a x)

Let's not care about any meta unless we say otherwise:

instance {-# OVERLAPPABLE #-} FromFormData' a => FromFormData' (M1 i c a) where
  fromFormData' = fmap M1 . fromFormData'

Sum and product:

instance (FromFormData' f, FromFormData' s) =>
         FromFormData' (f :*: s) where
  fromFormData' form = liftA2 (:*:) (fromFormData' form) (fromFormData' form)

instance (FromFormData' l, FromFormData' r) =>
         FromFormData' (l :+: r) where
  fromFormData' form =
    fmap L1 (fromFormData' form) <|> fmap R1 (fromFormData' form)

Writing an instance

Base case:

-- Note, overlaps instance for M1, because S1 = M1 S
instance Selector m =>
         FromFormData' (S1 m (Rec0 Text)) where
  fromFormData' form =
    let key = selName (undefined :: S1 m t p)
    in case M.lookup (T.pack key) form of
         Just [Just txt] -> Just $ M1 $ K1 txt
         _ -> Nothing
  • We don't have any value of the needed type to give to selName.
  • selName only needs the type of the value to work.
  • S1 m t p and S1 m (Rec0 Text) p are both fine, since selector name depends on m and not t.

What else can we build?

  • Show
  • Ord
  • Eq

What can't be built with just Generic?

fmap :: Functor f => (a -> b) -> f a -> f b

What else can we build?

Generic is a class for types of kind *, for * -> * there is

class Generic1 f where
  type Rep1 f :: * -> *
  from1 :: f a -> Rep1 f a
  to1 :: Rep1 f a -> f a
  
newtype Par1 p = Par1 { unPar1 :: p } -- parameter
newtype Rec1 f p = Rec1 { unPar1 :: f p } -- recursive occurrence

What else can we build?

data Expr a
  = Var Text | Const a | S (Expr a) (Expr a)
  deriving (Generic, Generic1)
λ> :kind! (Rep1 Expr)
(Rep1 Expr) :: * -> *
= D1
    ('MetaData "Expr" "Main" "main" 'False)
    (C1
       ('MetaCons "Var" 'PrefixI 'False)
       (S1
          ('MetaSel ...)
          (Rec0 Text))
     :+: (C1
            ('MetaCons "Const" 'PrefixI 'False)
            (S1
               ('MetaSel ...)
               Par1)
          :+: C1
                ('MetaCons "S" 'PrefixI 'False)
                (S1
                   ('MetaSel ...)
                   (Rec1 Expr)
                 :*: S1
                       ('MetaSel ...)
                       (Rec1 Expr))))

Questions?

Talk: https://www.koterpillar.com/instances-for-everyone

Source code

Links: